Inertial parameter estimation
2015-05-07
This was a course project for 16-711 Kinematics, Dynamics, and Control at Carnegie Mellon University.
The objective is to find the mass, moment of inertia in roll axis, and moment of inertia in pitch axis, and center of mass in the ground plane for a self-driving car using only onboard camera and lidar passively just by driving around. Obviously, this isn’t the best way to estimate vehicle inertial parameters, and requires making lots of assumptions, but it was fun.
1 Introduction
With the rise in proliferation of autonomous vehicles such as the Google Self-Driving Car google, issues of safety are increasingly relevant and important. In particular, determining the vehicle inertial parameters is important for effective control and accurate motion simulation. These vehicles often contain a lidar sensor for localization and obstacle avoidance. As such, the lidar sensor is an obvious choice for determining said inertial parameters.
Numerous studies have addressed the problem of determining inertial parameters in both the online and offline settings by using a variety of different sensors and techniques. Rajamani and Hedrick proposed in 1995 a method for inferring vehicle mass by observing the suspension, for example by directly measuring suspension travel using LVDTs rajamani. Several studies have investigated solving this problem in the online setting with accelerometers using various filtering techniques bestwenzelvahidiwinstead. The present study uses base excitation dynamics, which has also been studied by Pence et al in 2009 pence using acceleromaters and in the theoretical setting by Rozyn and Zhang 2010 rozyn and Kolansky and Sandu kolansky. My work is most similar to that of Rozyn and Zhang rozyn in that it uses a known terrain profile and suspension parameters. However, to my best knowledge, there has been no study using the lidar sensor to provide such a terrain profile.
2 Model and implementation
The problem statement is: Given lidar sensor input as point clouds sampled at discrete time steps, the vehicle geometry (wheelbase and track
), and suspension stiffness
and damping
, the output is the mass
, the roll moment of inertia
, the pitch moment of inertia
, and the center of gravity in the plane
.
The model used is a three degree of freedom base excitation model, with the state being pitch , roll
, and bounce
. It is assumed that the front and rear suspensions behave linearly and have identical parameters
,
, and that unsprung mass is negligible. Furthermore, it is assumed that the vehicle is travelling at a mostly constant velocity forwards, and that roll and pitch angles are small. No information about the yaw and lateral motion is obtained or inferred.

The equations of motion are
where the forces are given by a parallel spring damper approximation:
The algorithm used can be summarized as such:
- The generalized iterative closest point algorithm (GICP) gicp is used to determine the relative transformation between synchronized and rectified point clouds produced by the lidar sensor.
- At each time step, the suspension travel is determined using a ray shooting method.
- Inertial parameters are inferred from the suspension travel as a function of time.
The implementation of the GICP algorithm used in this study is provided by the Point Cloud Library pcl. For ray shooting, the lidar sensor clearly cannot see directly beneath the vehicle. As such, the point cloud is aggregated over 100 time steps (50 before and 49 after the current timestep) of 0.1~s each for a total duration of 10~s. Vertical rays are computed from the known relative position from the wheels to the lidar sensor, and all points within 20~cm of each ray are obtained. The suspension travel distance is then determined by the median of those points.
For inertial parameter estimation, the cost function is defined as the Euclidean distance, for all time steps, between the left and right sides of Equations 1, 2, 3, where the left side is computed from twice numerical differentiation of the pose data and the right side is obtained from Equation 4 using the ray shooting method to determine , where
is computed from central differences. A simplex method provided by MATLAB’s
fminsearch function is used to search over to minimize this error while
are computed using least squares given
.
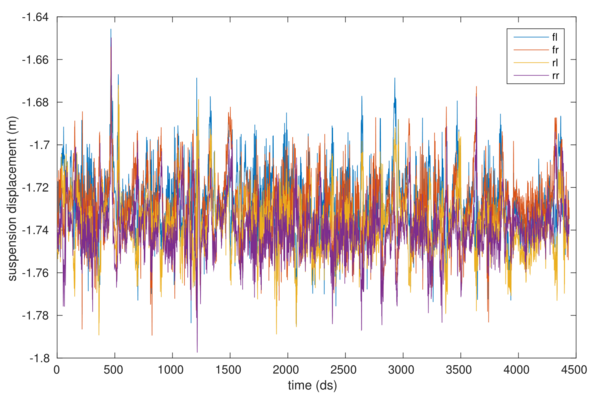
3 Results

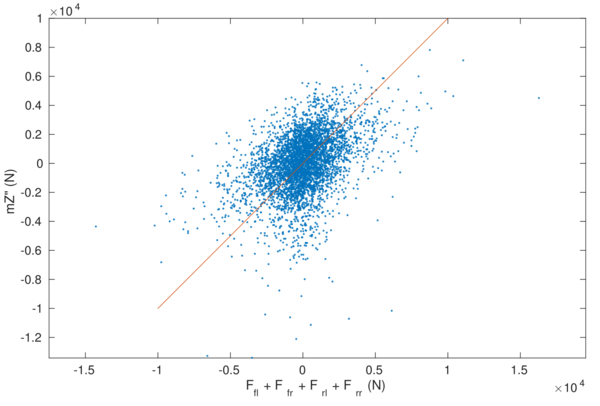
The algorithm is tested on the KITTI data set kittikittiikittiii, namely Sequence 00 of the Odometry data. The lidar point clouds are provided at a rate of 10~Hz, with about points per timestep. The sensor is a Velodyne HDL-64E mounted atop a Volkswagen Passat B6 station wagon. It is known that for this vehicle,
~m and
~m.
Assuming that ~N/m and
~kg/s, and using
~m as an initial guess, then the output of the program is:
These look like reasonable values since the mass is expected to be over 1400~kg passat and the moment of inertia in the pitch axis is clearly much higher than the one in the roll axis. The center of mass is close to the center of the vehicle and is closer to the front than the rear, which is expected since the car is front-engined.
4 Discussion
From Figure 4, it is clear that the data is extremely noisy. This could significantly affect the performance of the algorithm. The noise may arise from the fact that the assumptions in the model might not hold if the vehicle is being driven aggressively, or if there are nonlinear or hysteresis behaviour in the suspension. The KITTI dataset’s data rate of 10~Hz is too low to capture high frequency behaviour in the suspension. Using an inertial measurement unit or a high framerate camera, the pose of the vehicle can be more accurately determined with finer temporal resolution, allowing for better estimates of acceleration.
5 Conclusion
An algorithm is presented for the novel application of an onboard lidar sensor to the problem of determining the mass, center of mass in the plane, and moments of inertia in the roll and pitch axes. Testing on data on a Volkswagen Passat B6 equipped with a Velodyne HDL-64E sensor resulted in values close to expectations, despite the noisy nature of the data.
- rajamani Rajamani, Rajesh, and J. Karl Hedrick. “Adaptive observers for active automotive suspensions: theory and experiment.” Control Systems Technology, IEEE Transactions on 3.1 (1995): 86-93.
- best Best, Matt C., T. J. Gordon, and P. J. Dixon. “An extended adaptive Kalman filter for real-time state estimation of vehicle handling dynamics.” Vehicle System Dynamics 34.1 (2000): 57-75.
- wenzel Wenzel, Thomas A., et al. “Dual extended Kalman filter for vehicle state and parameter estimation.” Vehicle System Dynamics 44.2 (2006): 153-171.
- vahidi Vahidi, Ardalan, Anna Stefanopoulou, and Huei Peng. “Recursive least squares with forgetting for online estimation of vehicle mass and road grade: theory and experiments.” Vehicle System Dynamics 43.1 (2005): 31-55.
- winstead Winstead, Vincent, and Ilya V. Kolmanovsky. “Estimation of road grade and vehicle mass via model predictive control.” Control Applications, Proceedings of 2005 IEEE Conference on. IEEE, 2005.
- pence Pence, Benjamin L., Hosam K. Fathy, and Jeffrey L. Stein. “Sprung mass estimation for off-road vehicles via base-excitation suspension dynamics and recursive least squares.” American Control Conference. ACC’09. IEEE, 2009.
- rozyn Rozyn, Matthew, and Nong Zhang. “A method for estimation of vehicle inertial parameters.” Vehicle system dynamics 48.5 (2010): 547-565.
- kolansky Kolansky, Jeremy, and Corina Sandu. “Real-time parameter estimation study for inertia properties of ground vehicles.” Archive of Mechanical Engineering 60.1 (2013): 7-21.
- google Google Self-Driving Car Project, \
https://plus.google.com/+GoogleSelfDrivingCars/. Retrieved May 7, 2015. - gicp Segal, Aleksandr, Dirk Haehnel, and Sebastian Thrun. “Generalized-ICP.” Robotics: Science and Systems. Vol. 2. No. 4. 2009.
- pcl Rusu, Radu Bogdan and Steve Cousins. “3D is here: Point Cloud Library (PCL).” IEEE International Conference on Robotics and Automation (ICRA) May 9, 2011.
- kitti Geiger, Andreas, Philip Lenz, and Raquel Urtasun. “Are we ready for Autonomous Driving? THe KITTI Vision Benchmark Suite.” Conference on Computer Vision and Pattern Recognition (CVPR). 2012.
- kittii Geiger, Andreas, Philip Lenz, Cristoph Stiller, and Raquel Urtasun. “Vision meets Robotics: The KITTI Dataset.” International Journal of Robotics Research (IJRR). 2013.
- kittiii Fritsch, Jannik, Tobias Kuehnl, and Andreas Geiger. “A New Performance Measure and Evaluation Benchmark for Road Detection Algorithms.” International Conference on Intelligent Transportation Systems (ITSC). 2013.
- passat Technical characteristics: Volkswagen - Passat Variant (B6). \
http://www.auto-data.net/en/?f=showCar&car_id=8901. Retrieved May 7, 2015.