1 Introduction

A Lie group is a group that deals with manifolds. What is a manifold and what is a group?

When we think about geometry, most of us think about geometry in a Euclidean space. A Euclidean space has many nice properties. One property is that, if you travel in one direction, you keep going in that direction, and never find yourself going in another direction. A good example is the 2D Euclidean space . If you’re travelling in the -direction, the -coordinate couldn’t care less!

In a Euclidean space, you can also keep travelling in a particular direction and never come back to where you started.

However, there are some spaces that are non-Euclidean. For example, imagine standing on the surface of a sphere. If you’re standing in San Francisco facing north, and you keep walking forwards, you’ll eventually find yourself in Kazakhstan, which is in the Eastern hemisphere, even though you started out in the West! And then if you go even further, you’ll end up right where you started!

A manifold is a space that may not be Euclidean, but sure looks Euclidean in a small area around you. In the sphere example, the small area around you looks pretty much just like a flat plane, which is Euclidean! Cue the flat Earther jokes!

A group is a set that has some operation to combine two things in the group to make a third thing, so that:

• closure: is still in the group
• associativity:
• identity: there is an identity element such that
• inverse: for every , there is an so that .

A matrix group uses matrix multiplication for so that it automatically satisfies the last three requirements.

A Lie group is a group that is also associated with a Lie algebra to help us deal with manifolds. If we proceed with the analogy of standing on a the spherical Earth…

• The Lie algebra handles the locally Euclidean stuff on the manifold, like walking forwards or walking left while on a spherical Earth.
• The Lie group deals with bigger motions, like an intercontinental flight, where you can no longer assume a flat Earth.

Before we get into details, let us begin with an example.

2 Rotations in 2D

Now we can start with an example of a classical Lie group called , which stands for the special orthogonal group. Put simply, this is a 2D rotation.

2D rotations are not Euclidean, because if you rotate by 360 degrees, you’ll end up at the same place, which is something that cannot happen in a Euclidean space. However, locally, they are like , a trivial 1-dimensional Euclidean space.

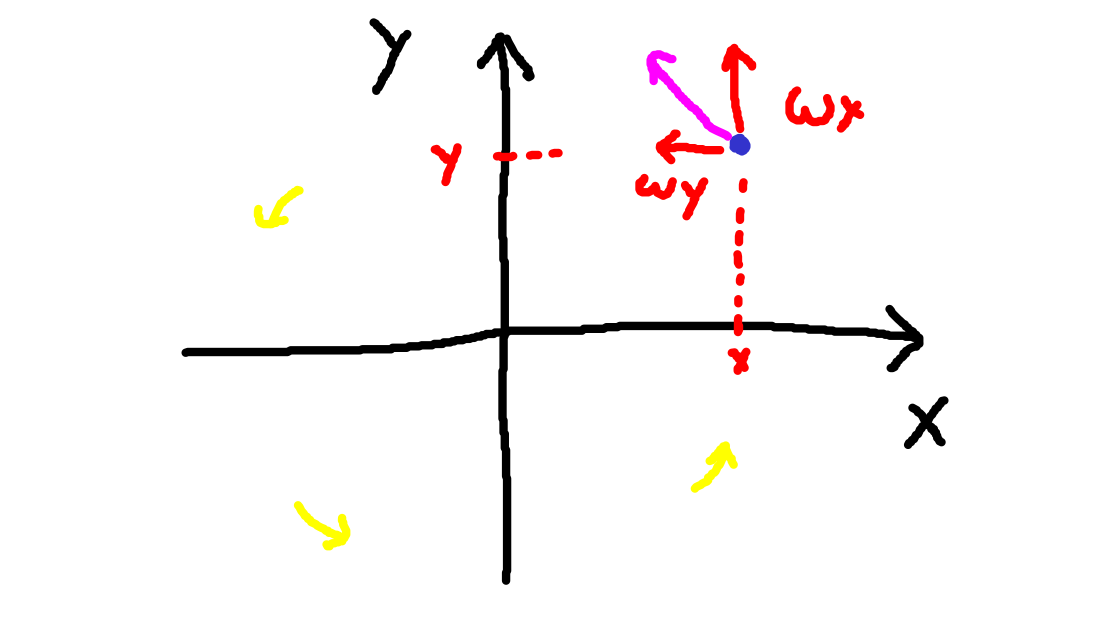
Imagine a point

1

and we want to rotate it anticlockwise a little bit, by a small angle . How does the point’s position change?

Well, first we study how it changes depending on the point’s position.

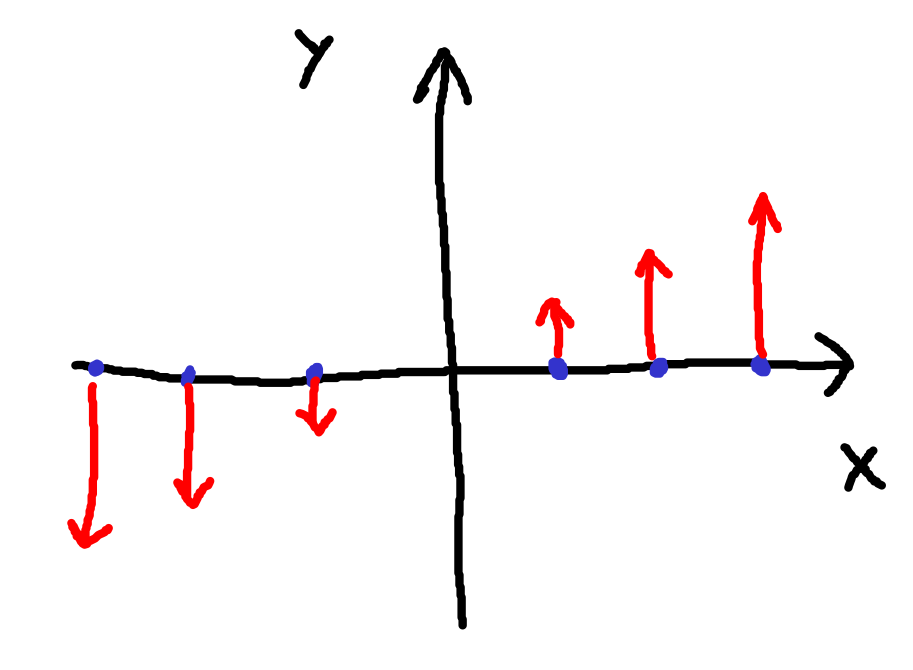
As you can see, the more the -coordinate, the more the -coordinate increases. Yet, the way its -coordinate changes doesn’t depend on its previous -coordinate at all.

So we can write:

2

Likewise, the more the -coordinate, the more the -coordinate decreases.

So we can write:

3

In matrix notation,

4

Well, that’s cool, but we’ve only rotated it by a tiny amount. To rotate it by a nontrivial amount, we need to do it a bunch of times!

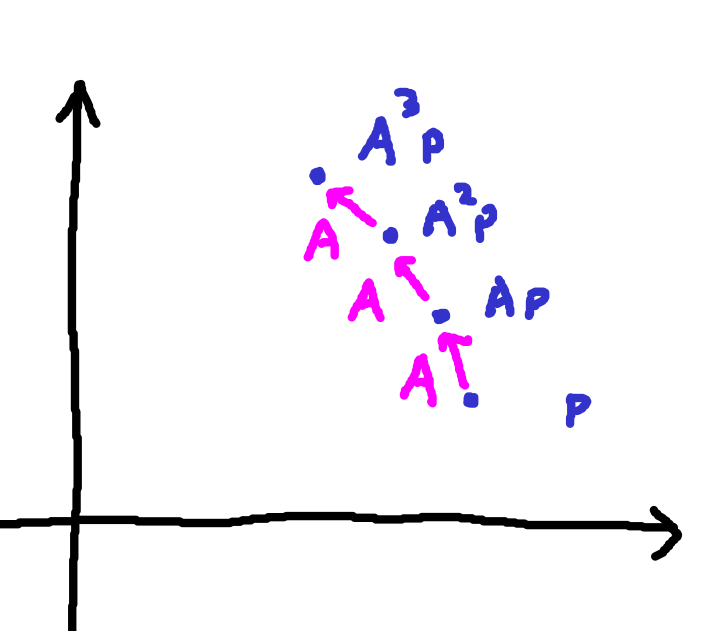
Suppose we actually want to rotate things by an angle . We can make the tiny amount be a small fraction of , say,

5

Then, to rotate it by the full angle , we’d need to apply it times. The biggger the , the better!

6

Let’s define the generator :

7

So the rotation matrix is:

8

To find the limit, we can use the binomial theorem:

9

But then as approaches infinity, all the s cancel out. We use the monotone convergence theorem and apply the limit to each term, e.g. the third one:

10

Now we’re left with:

11

Notice it is the Taylor expansion of the exponential function.

This is called the exponential map, and the Taylor series definition applies to all Lie groups.

12

In the case of 2D rotations, we can sum up this series with a closed form.

Notice that:

13

Then we group odd and even terms and notice they resemble the Taylor series of cosine and sine,

14

Hooray, we’ve just derived the rotation matrix!

To recap:

• The rotation matrix is in the Lie group .
• The matrix is in the Lie algebra , which is of dimensionality 1 and behaves just like . The value represents the angle of how much you’re rotating. The local space that is sort of Euclidean-ish is known as the tangent space. In this case, as you’ve seen from the pictures, it literally resembles the tangent of a circle.
• The exponential map relates the two:

The astute reader will notice many similarities between this exercise and imaginary numbers. Indeed, an imaginary number , representing an angle, is related to rotation in the form of in much the same way.

3 Rotations in 3D

Unlike in 2D, we can now rotate things in three axes.

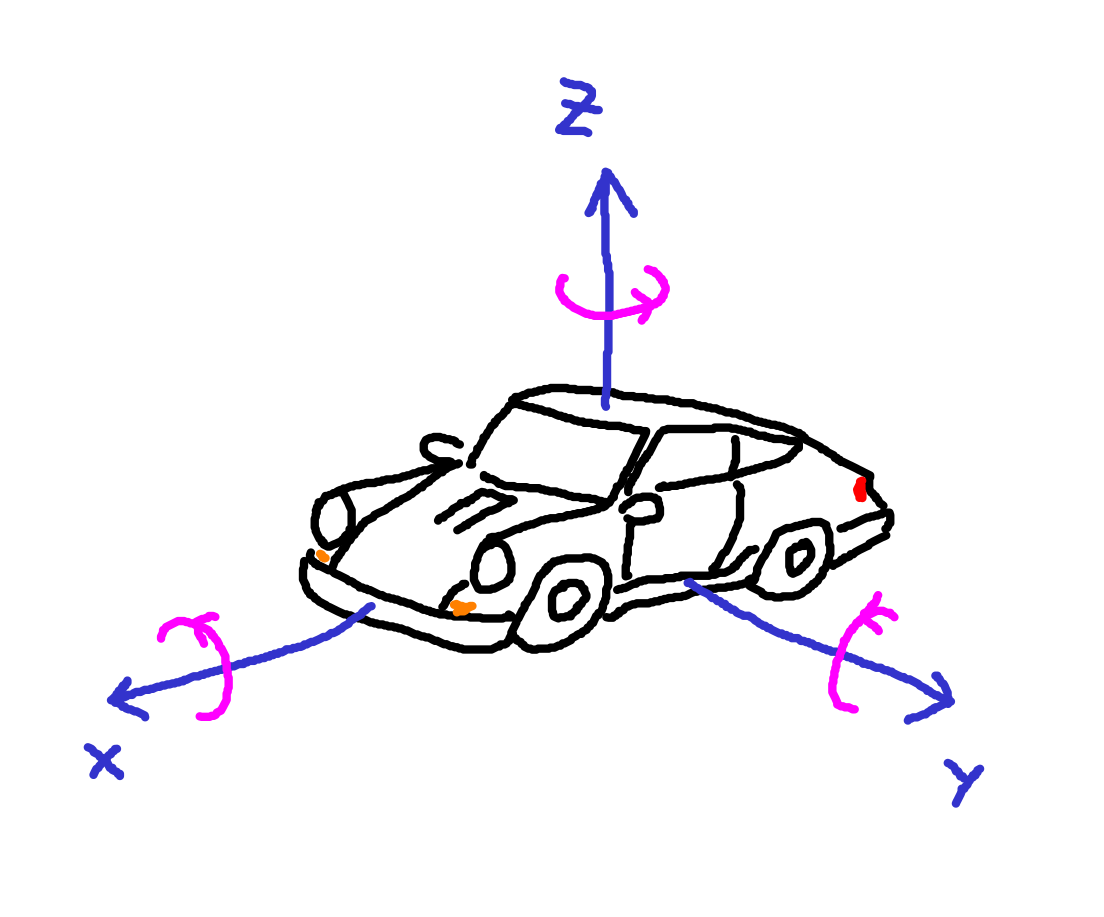
Based on the same idea as previously, we can think about what happens if we rotate stuff slightly by around the -axis. Well, the point’s -coordinate remains unchanged, but its - and -coordinates change in exactly the same way as previously.

15

Notice the top-left submatrix is exactly the same as in the previous section.

We can likewise derive:

16

Then, an element is the skew-symmetric matrix:

17

Note that the matrix is called the “cross-product matrix” because

18

The exponential can be computed again by grouping odd and even terms of the Taylor series.

19

This is called the Rodrigues’ rotation formula.

The vector is also called the axis-angle representation because its norm represents the angle, while the normalised vector is the axis of rotation.

Interestingly, in all the examples we’ve looked at so far, we’re dealing with spheres whose surfaces look like planes of one fewer dimension.

• for 2D rotations, the 1D rotation angle is the tangent space of a 2D circle. We discussed an analogy to imaginary numbers
• the Little Prince is on a 3D sphere whose tangent space is a 2D plane
• here the 3D tangent space is related to a 4D sphere! The 4D sphere is known as unit quaternions, an extension of imaginary numbers

Just like how a 3D sphere has , a unit quaternion representing must have .

3.1 Implementations of 3D rotations

The Lie Group SO(3) is a group of rotation matrices, but we can implement it in many ways.

For example we could imagine there being an abstract trait SO3 in your favourite programming language, supporting common operators such as rotate_point, compose, log, and so on.

The following is Rust-like pseudocode.

trait SO3 {
    fn from_so3(so3: &Point3) -> Self;
    fn rotate_point(&self, point: &Point3) -> Point3;
    fn compose(&self, other: &Self) -> Self;
    /* ... and so on ...*/
}

impl SO3 for Mat3 {
    fn from_so3(so3: &Point3) -> Self {
        // TODO: implement Rodrigues formula here lol
    }
    fn rotate_point(&self, point: &Point3) -> Point3 {
        // using matrix multiplication
        self * point
    }
    fn compose(&self, other: &Self) -> Self {
        // using matrix multiplication
        self * other
    }
}

impl SO3 for Quaternion {
    fn from_so3(so3: &Point3) -> Self {
        let half_theta = so3.norm() / 2.0;
        let s = theta.sin();
        let c = theta.cos();
        Self::new(s * so3.x, s * so3.y, s * so3.z, c)
    }
    fn rotate_point(&self, point: &Point3) -> Point3 {
        // using quaternion multiplication
        let q = Quaternion::new(point.x, point.y, point.z, 0.0);
        self.conjugate() * q * self
    }
    fn compose(&self, other: &Self) -> Self {
        // using quaternion multiplication
        self * other
    }
}

There are many other ways to implement SO3 as explained on Wikipedia. Common ways to implement SO3 could include:

• axis angle, which is basically just
  • store the angle as the norm of the axis
  • store the angle separately from the axis, which is normalized
  • store the tangent of the angle (Gibbs vector)
• Euler angles, which have the problem of Gimbal lock

Which parameterisation of to use depends on what you want to do.

• Transforming many points with the same rotation? Use a rotation matrix
• Composing rotations often? Quaternion
• Controlling a pan tilt camera? Euler angles

4 Rigid transformations SE(3)

The Special Euclidean Group deals with rigid transformations by combining a rotation in with a translation in .

20

Just like and , each element in is associated with an element on the corresponding Lie algebra, :

21

where is the cross product matrix of . We may also write it as a vector.

22

Some textbooks put the rotational part on top and some put it on the bottom; it doesn’t matter as long as you’re consistent.

In future blog posts we will use the and representations interchangeably depending on context.

A transformation is used to transform a 3D point :

23

The homogeneous representation adds a one at the end:

24

so that points may be transformed rigidly

25

5 Things to do with Lie groups

Lie groups provide us with elegant tools to do:

• Interpolation. For example the element between and is . With Lie groups, it’s possible to define all sorts of curves, such as splines, without running into pitfalls due to the non-Euclidean nature of things such as 3D rotations.
• Linearisation. Lie algebras allow us to differentiate with respect to small perturbations. This allows us to do non-linear least squares optimisation, as well as other estimation techniques based on linearisation, such as an extended Kalman filter.

In a next blog post we will cover optimization on the manifold of Lie groups for all kinds of robotics applications like SLAM!